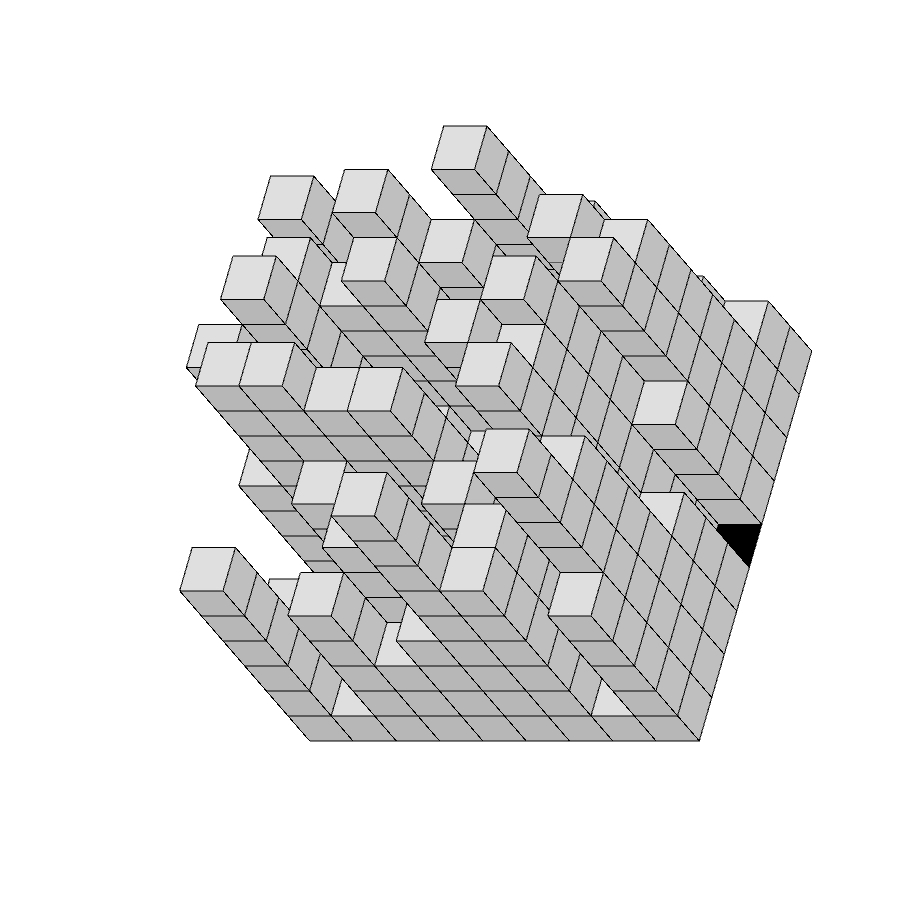
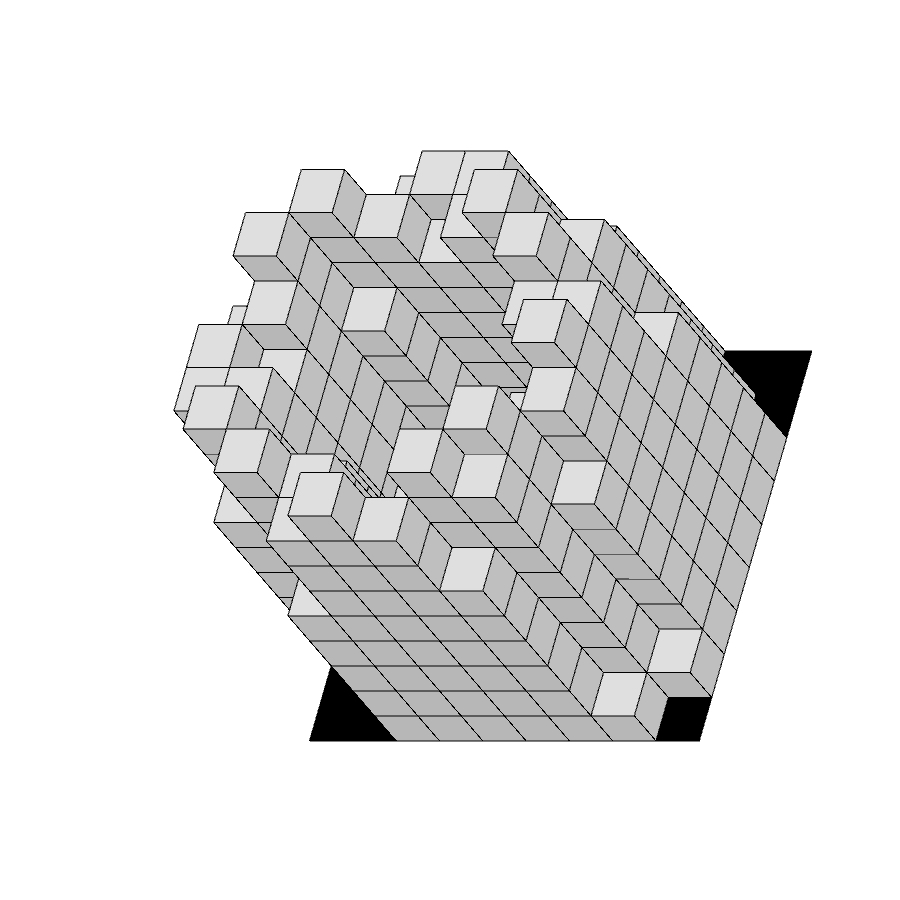
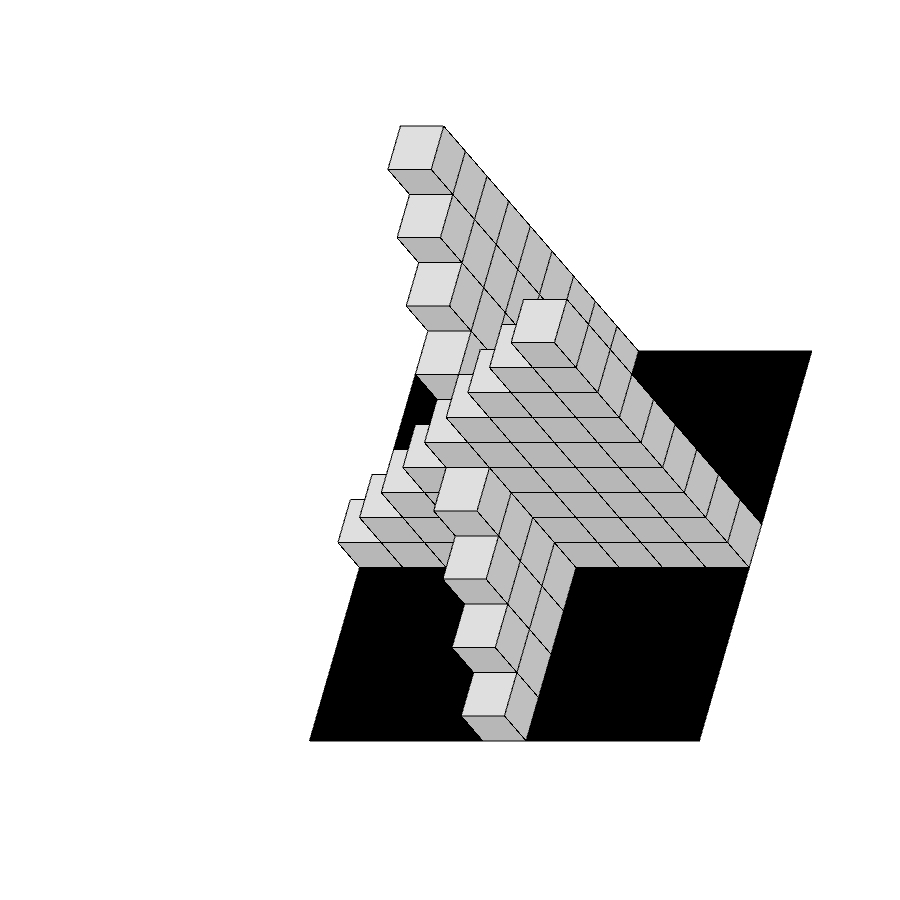
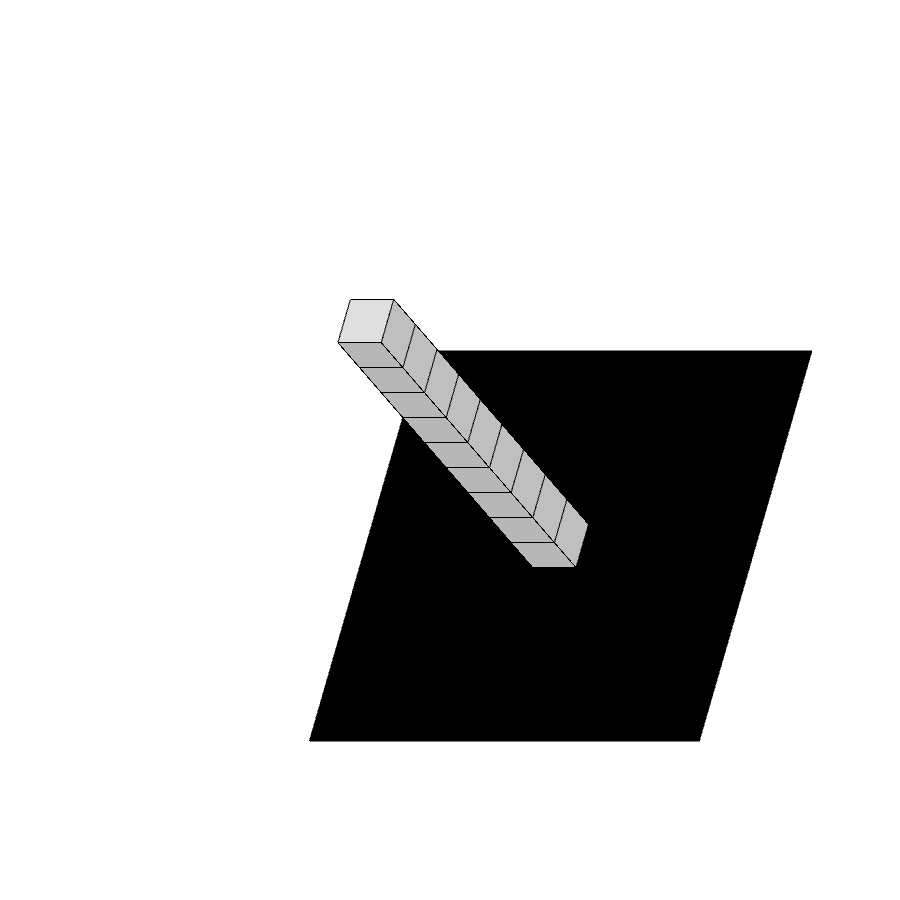
Uno spazio N x N x N è composto da N3cubetti.
9 x 9 x 9 = 729 cubetti.

Settecentoventinove sembra già un numero grande, ma se pensiamo alle possibili forme che possono essere rappresentate in questo spazio, i numeri diventano inaspettatamente immensi.
L’ordine di grandezza è addirittura simile al numero di atomi presenti nell’intero universo:
1081 configurazioni.
Vale a dire 10 miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di possibili forme diverse.
A ciascuno miliardi di forme
La quantità di forme è così grande che ogni essere umano potrebbe avere in esclusiva
1081/ 1010= 1071 configurazioni.
Lo scopo di questo progetto è di permettere ad ognuno di trovare la propria forma preferita tra miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di configurazioni.
Per chiarezza, definiamo “forma” ogni configurazione di “pilastri” come quelli nella figura qui sopra. Escludiamo dal campo di ricerca le configurazioni che non appoggiano sulla base. Senza questa approssimazione le possibili configurazioni sarebbero molte di più, come illustrato nell’Appendice 1.
Necessità di un metodo
Trovare la propria forma preferita in mezzo a così tante possibilità non è affatto semplice.
Se ad esempio volessimo assegnare un indice di gradimento, dedicando un secondo ad ogni possibile forma, ci servirebbe un tempo immenso:
3 x 1074anni.
In confronto i 13 miliardi di anni dal Big Bang ad oggi sembrerebbero un’infinitesima frazione di secondo.
Anche escludendo tutte le forme simmetriche o in qualche modo equivalenti resteremmo nell’ordine dei miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di anni.
Fortunatamente la tecnologia ci viene in aiuto: se riuscissimo a trasferire il nostro “ideale” di forma ad un calcolatore, potremmo concentrarci solo su sottoinsiemi di configurazioni e trovare in tempi umani la nostra forma preferita.
Capire meglio i numeri in gioco
Per comprendere meglio i numeri in gioco riporto un esempio molto semplice: la targa della vostra auto.
In Italia il formato è il seguente:
AA 999 AA.
Quanti valori unici possono essere rappresentati? La risposta è abbastanza semplice:
25×25 x 10x10x10 x 25×25.
Che corrisponde a:
390.625.000 targhe diverse.
Ma soffermiamoci per semplicità sull’elemento numerico:
999
Per sapere quante diverse combinazioni di numeri decimali possono essere rappresentati è sufficiente eseguire il calcolo:
10x10x10 = 103= 1000.
Infatti con tre cifre decimali (che possono cioè assumere dieci valori: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) possiamo rappresentare mille numeri che vanno da 000 a 999. Se usassimo tre cifre binarie (che possono cioè assumere solo i valori 0 e 1) potremmo rappresentare solo otto numeri: 000, 001, 010, 011, 100, 101, 110, 111.
2x2x2 = 23= 8.
In teoria quindi nel nostro spazio 9x9x9 (fatto da 729 cubetti), considerando che ogni cubetto può essere pieno o vuoto (e quindi gli stati possibili sono solo 0 e 1) potrebbero starci:
2729 pari a circa 10219forme diverse.
Un numero immenso, che diventerebbe ancora più grande se considerassimo ad esempio 3 colori possibili per il cubetto:
3729 pari a circa 10247forme diverse.
Per questo, ho deciso di “limitare” il campo di questa ricerca all’incirca al numero di atomi nell’universo, prendendo in considerazione solo le forme costituite da pilastri che appoggiano sulla base. In numeri, è come se avessimo
9×9 = 81 cifre della matrice
a cui assegnare valori da 0 a 9, cioè 10x10x…x10 (81 volte) pari a:
1081configurazioni possibili.