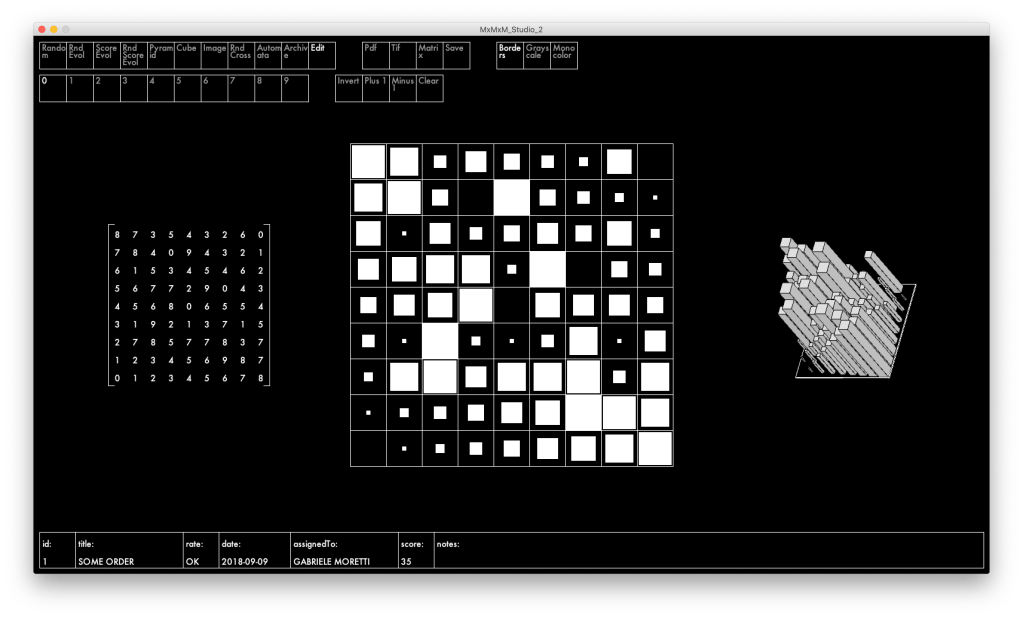
La rappresentazione fisica deve essere efficace sia nella versione bidimensionale sia in quella tridimensionale. In questo modo sarà molto rapido e semplice visualizzare le forme su monitor o su carta.
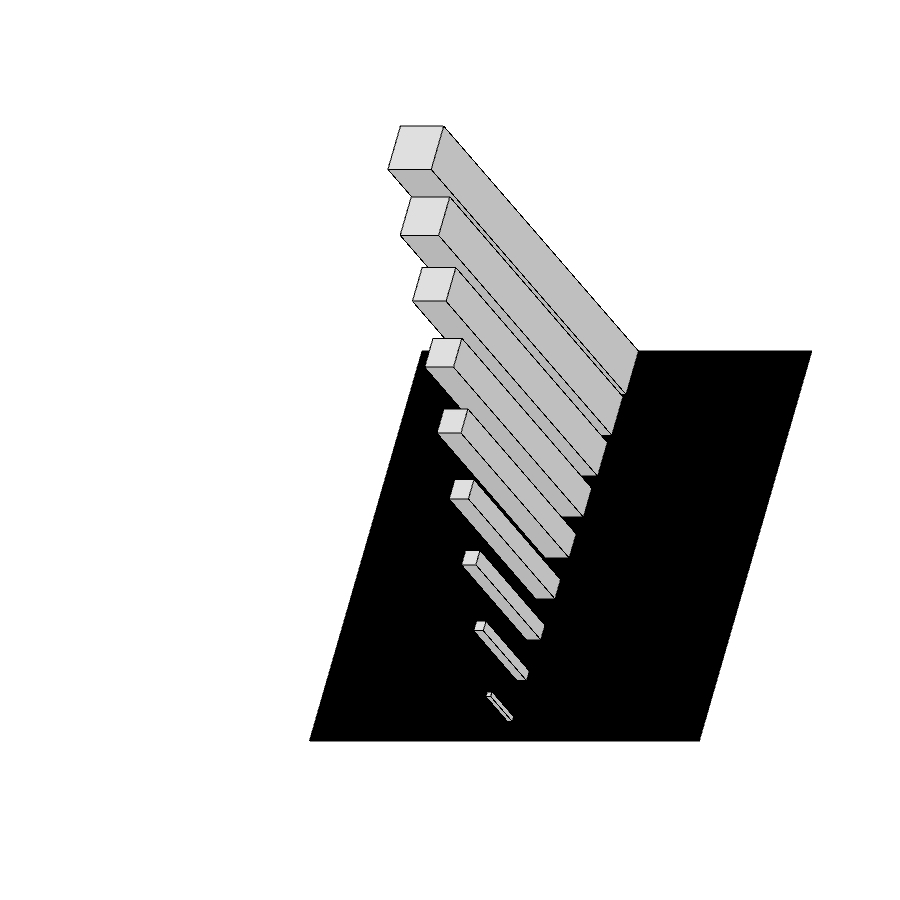
Per i pilastri utilizzeremo dei semplici parallelepipedi bianchi, alti quanto il valore intero che rappresentano e con la base proporzionale allo stesso valore.
Supponendo che l’intero spazio 9x9x9 abbia il lato di 81 cm, segue la tabella che riporta le dimensioni dei parallelepipedi che rappresentano i pilastri.
| Valore | Altezza | Lato quadrato |
| 0 | 0 | 0 |
| 1 | 9 cm | 1 cm |
| 2 | 18 cm | 2 cm |
| 3 | 27 cm | 3 cm |
| 4 | 36 cm | 4 cm |
| 5 | 45 cm | 5 cm |
| 6 | 54 cm | 6 cm |
| 7 | 63 cm | 7 cm |
| 8 | 72 cm | 8 cm |
| 9 | 81 cm | 9 cm |
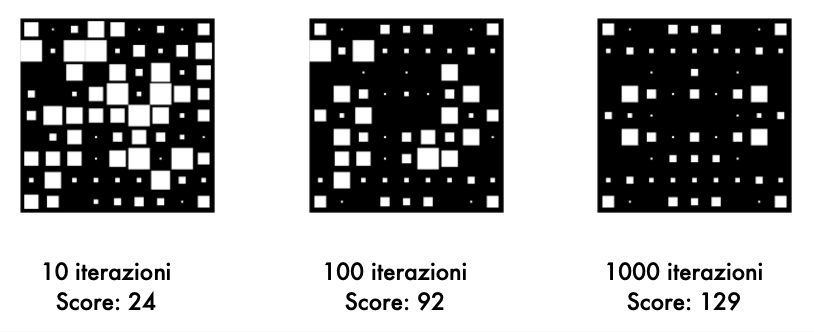
Questo semplice linguaggio ci permette di creare un trait d’union tra noi e il calcolatore: il computer vede una matrice di numeri interi e noi vediamo pattern emergenti che siamo in grado di classificare con uno sguardo.










Leave a comment